三平方の定理 計算 角度 656544-三平方の定理 計算 角度
直角三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と角度 斜辺と高さ 斜辺と角度 高さと角度 面積と底辺 面積と高さ 面積と斜辺 面積と角度
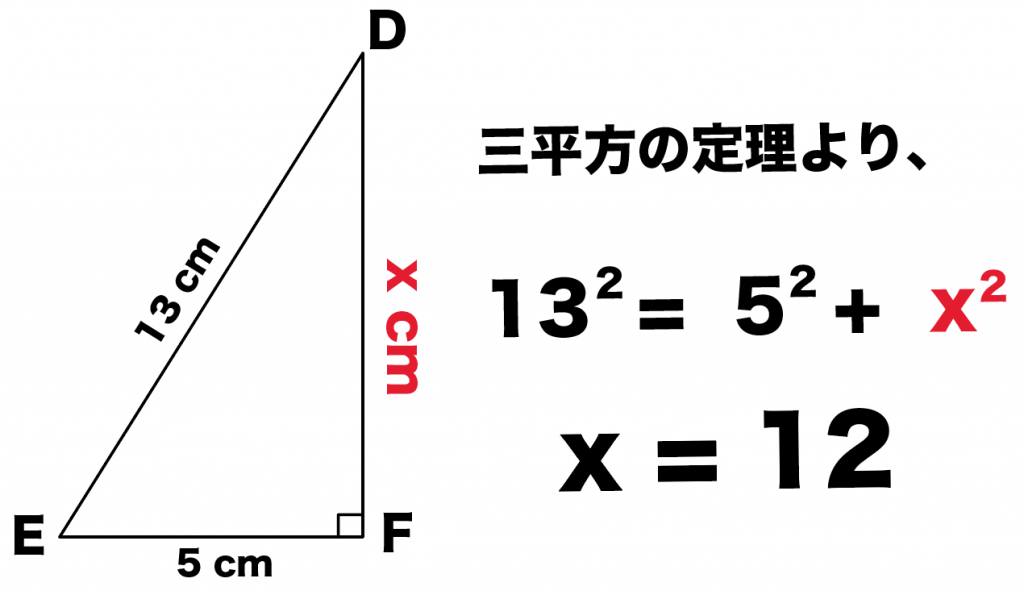
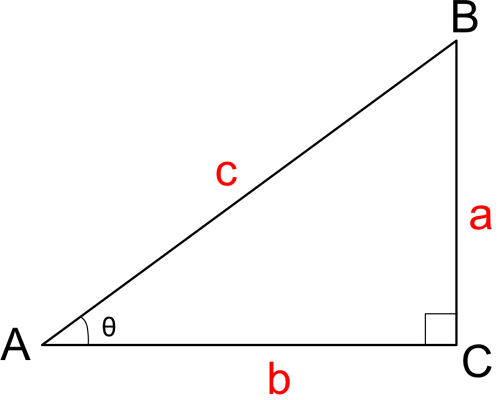
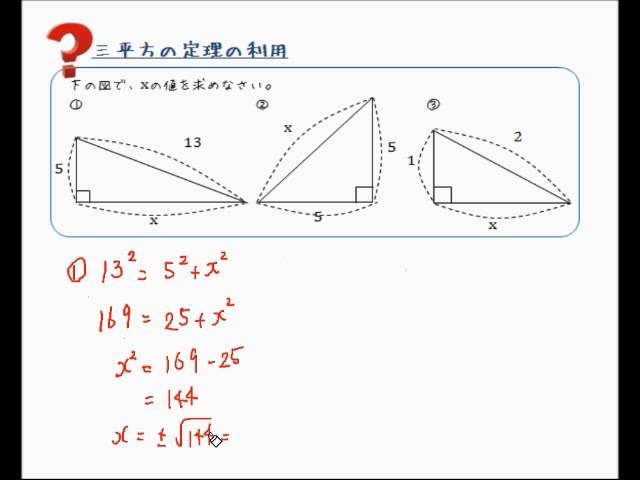
三平方の定理 計算 角度-三平方の定理は、 直角三角形の三辺をa,b,cとする。 斜辺 (最も長い辺)をcとすると、 c² = a² b² が成り立つ というものです。 別名ピタゴラスの定理とも呼ばれます。 式は綺麗ですが、二乗が出てきます。 なので、実際にこの定理で辺の長さを計算すると、平方根を求める作業が必要になり、大変かもしれません。 三平方の定理の計算問題の解き方 斜辺以外の辺を求める問題 斜辺以外の辺を求めるときも、同様に公式に当てはめるだけです。 例題 上図の三角形の辺の長さxを求めよ x>0より x=12が答えになります。 慣れてきたら一気に と立式してしまいましょう。
三平方の定理 計算 角度のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
 |  | |
「三平方の定理 計算 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「三平方の定理 計算 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 | ||
「三平方の定理 計算 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
 |  |  |
「三平方の定理 計算 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「三平方の定理 計算 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
 |  | |
「三平方の定理 計算 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「三平方の定理 計算 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 | ||
「三平方の定理 計算 角度」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | 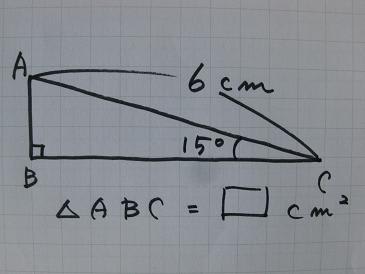 |
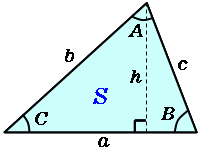
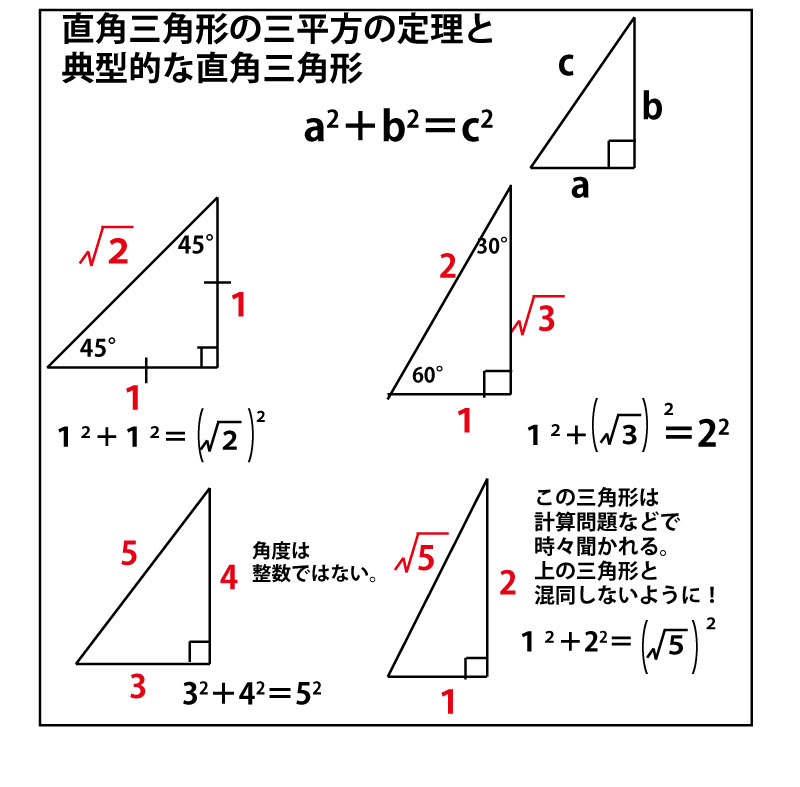
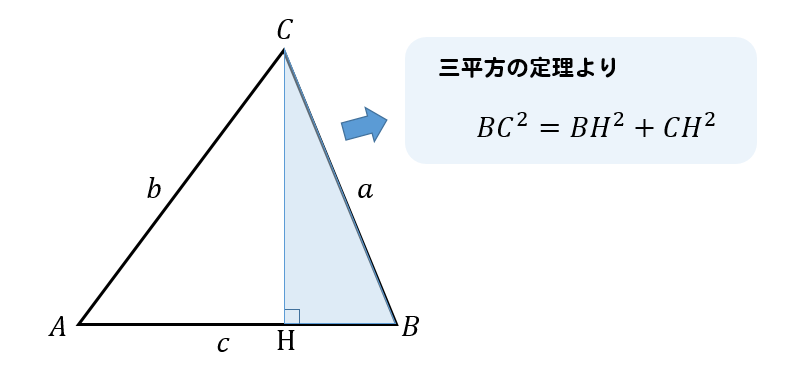
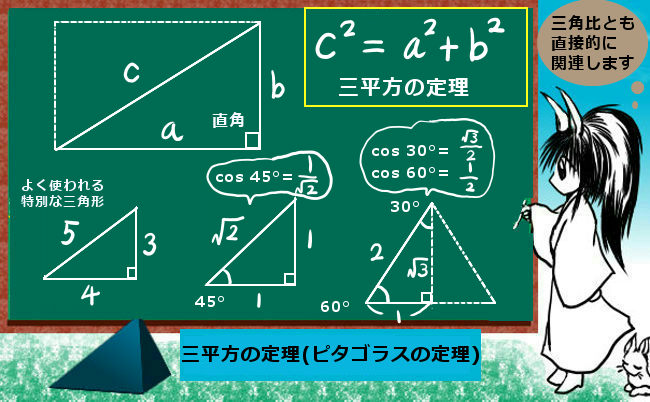
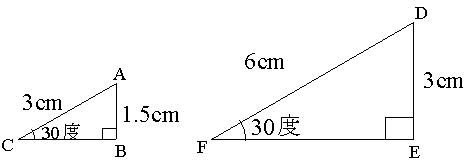
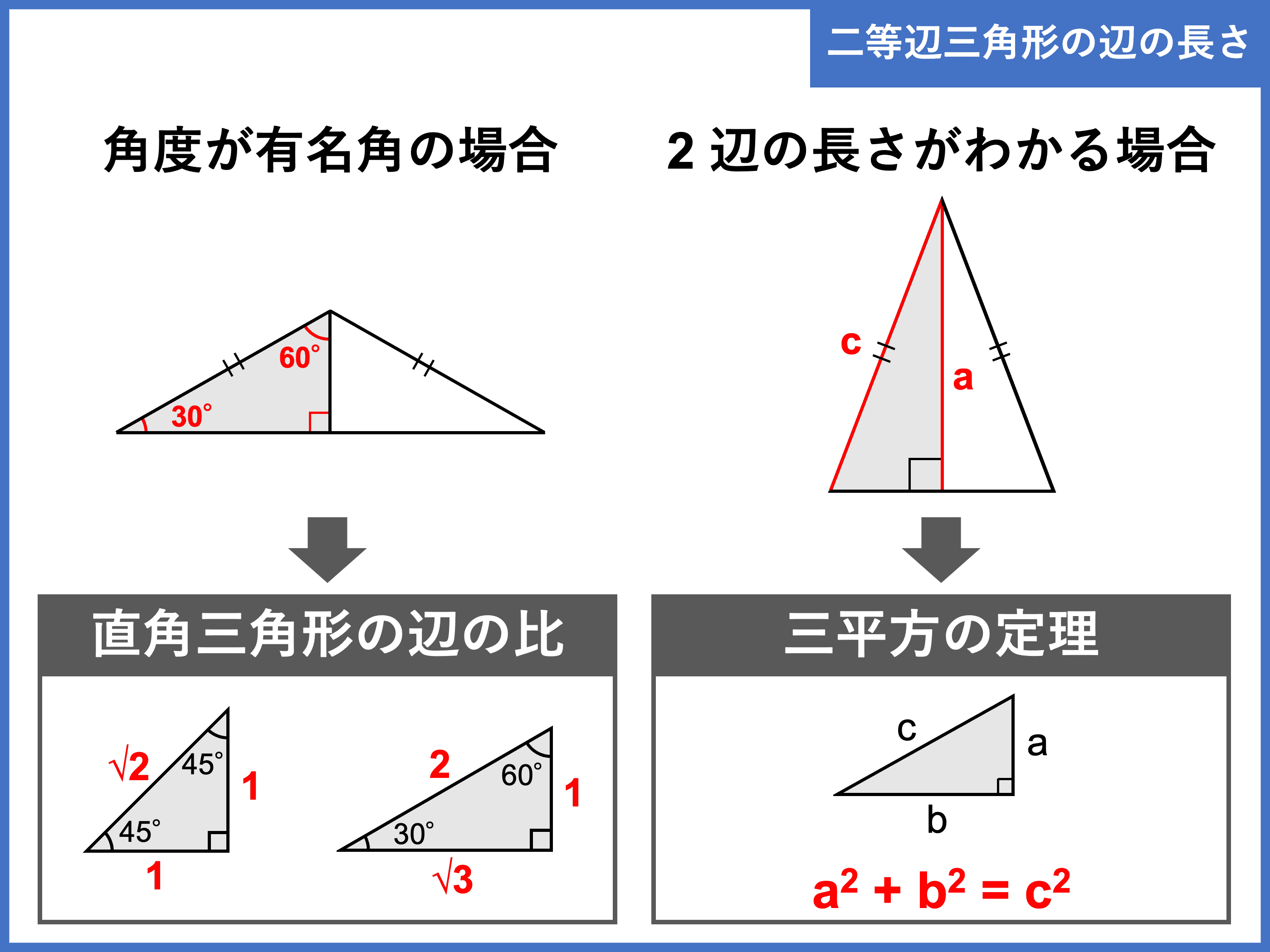
高さというのは、「頂点から底辺に下した垂線の長さ」のことでした。 垂線と言うことはまた直角三角形がどこかに現れそうですね! 解答 A B D A B D は直角三角形なので、三平方の定理(ピタゴラスの定理)より、 3 2 h 2 = 6 2 3 2 h 2 = 6 2 この式を整理すると、 h 2 = 36 − 9 = 27 h 2 = 36 − 9 = 27 h > 0 h > 0 なので、 h = √ 27 = 3 √ 3 ( c m) h = 27 = 3 3 ( c m) また、 三平方の定理とは? 証明や計算問題、角度と辺の比の一覧 21年10月21日 この記事では「三平方の定理」について、その公式や計算方法をできるだけわかりやすく解説していきます。 また、三平方の定理の証明や、暗記が必要な角度と辺の比などについても紹介していきますので、この記事を通してぜひマスターしてくださいね。 目次 非表示 三平方の定理とは
Incoming Term: 三平方の定理 計算 角度,
No comments: